Programación científica
Cálculo científico
1. Presentación
El cálculo científico es un dominio muy particular de la informática, que tiene sus propias exigencias y necesidades específicas. Además no solo está destinado para los matemáticos https://es.wikipedia.org/wiki/N%C3%BAmero_primo_de_Mersenne
El cálculo científico toca dominios muy amplios, como el conjunto de áreas científicas (secuenciado de ADN, etc.), el análisis de imágenes, la cartografía, el análisis de sonido o vídeos, las matemáticas financieras, el control de robots, la generación de gráficos, la animación de vídeo, el análisis lingüístico, la lectura de texto por un autómata, etc. que son todos dominios de nicho. De hecho, las matemáticas están en todos lados y el cálculo científico, también.
Cualquier proyecto informático puede necesitarlo, incluido un proyecto que a priori no tenga nada que ver con el dominio de la ciencia, como un proyecto de gestión documental. En efecto, los sistemas de clasificación y las funciones de búsqueda de documentos, pueden utilizar el cálculo científico.
También se puede mencionar el ejemplo del retoque de imágenes o el difuminado de vídeo en tiempo real, que son dominios de aplicación del cálculo...
Tablas multidimensionales
1. Creación
Una tabla NumPy se puede crear a partir de una lista Python:
>>> a = array([2, 3, 4]) Atención: no hay que confundir esta tabla con la del módulo array.
Cuando se muestra esta tabla, se presenta en forma de lista:
>>> print(a)
[2, 3, 4] Pero se puede visualizar el tipo de los elementos que contiene:
>>> a.dtype
dtype('int64') Este resultado puede cambiar en función de su plataforma (y del compilador C que se encuentra detrás de su Python), pero tendrá un tipo entero. Si un solo número no es entero, tendrá un tipo real:
>>> b = array([1.2, 3.5, 5.1])
>>> b.dtype
dtype('float64') También se puede crear muy rápidamente tablas de varias dimensiones, a partir de listas de listas o de listas de n-tuplas:
>>> array( [ (1.5,2,3), (4,5,6) ] )
array([[ 1.5, 2. , 3. ],
[ 4. , 5. , 6. ]])
>>> array( [ ((1.5,2,3), (4,5,6)), ((1.5,2,3), (4,5,6)) ] )
array([[[ 1.5, 2. , 3. ],
[ 4. , 5. , 6. ]],
[[ 1.5, 2. , 3. ],
[ 4. , 5. , 6. ]]]) Durante la visualización, la segunda dimensión aparece gracias al salto de línea, la tercera gracias a dos saltos, lo que hace que aparezca una línea en blanco.
Como la herramienta es muy flexible, también se puede simplemente generar una lista con la ayuda de un generador, similar a range:
>>> arange(15)
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]) También se puede dar un paso:
>>> arange( 10, 30, 5 )
array([10, 15, 20, 25]) Pero también puede funcionar con números reales:
>>> arange( 0, 2, 0.3 )
array([ 0. , 0.3, 0.6, 0.9, 1.2, 1.5, 1.8]) Para terminar, una vez que se ha generado una lista de números, se puede reconstruir a voluntad, lo que nos permite crear tablas de varias dimensiones:
>>> arange(15).reshape(3, 5)
array([[ 0, 1, 2, 3, 4], ...Matrices
Si las tablas son objetos maleables que representan un conjunto de datos cualquiera, las matrices son objetos matemáticos con reglas estrictas.
Sin embargo, hay algunas similitudes entre las matrices y las tablas. NumPy permite manipularlas de manera muy sencilla.
A continuación se muestra cómo crear una matriz, a partir de una sencilla cadena de caracteres:
>>> A = matrix('1.0 2.0; 3.0 4.0') Observe que el espacio sirve para separar los elementos de una misma línea y que el punto y coma sirve para separar las líneas entre ellas.
Cuando se muestra una matriz, esta se presenta siempre en forma de una lista de listas, pero esta vez tenemos matrix en lugar de array:
>>> A
matrix([[ 1., 2.],
[ 3., 4.]]) Se puede calcular la transposición de una matriz, de la siguiente manera:
>>> A.T
matrix([[ 1., 3.],
[ 2., 4.]]) A continuación se muestra una matriz en una línea:
>>> X = matrix('5.0 7.0')
>>> X
matrix([[ 5., 7.]]) Se transpone en una sola columna:
Y = X.T
>>> Y
matrix([[ 5.],
[ 7.]]) Se puede multiplicar una matriz cuadrada, por una matriz de columna del mismo tamaño:
>>> A*Y
matrix([[...Generación de gráficos
Python es un lenguaje que tiene muchas posibilidades. Se puede utilizar de manera imperativa o de manera orientada a objeto, sin ningún problema.
En lo que respecta a la generación de gráficos, se puede tanto llamar a una sintaxis pytónica que va a utilizar el objeto o bien preferir una sintaxis MATLAB, lo que es práctico para los que conocen este lenguaje, porque esto evita tener que volver a aprender todo y tener que controlar los conceptos de la orientación a objetos.
Para visualizar un gráfico, necesita utilizar una consola IPython o incluso mejor, IPythObservebook. Para este último, el comando recomendado para lanzarlo es:
$ ipython3 notebook --pylab inline 1. Sintaxis MATLAB
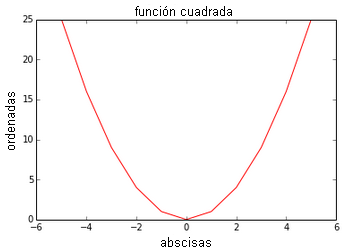
Para diseñar un gráfico, es suficiente con proceder por etapas. En primer lugar, se crea un espacio lineal:
>>> x = linspace(-5, 5, 11) Posteriormente, se crea la función a representar:
>>> y = x ** 2 Después, se crea nuestro espacio de representación:
>>> figure() Seguimiento del gráfico (queremos representar y respecto a x y queremos una línea roja):
>>> plot(x, y, 'r') Se puede dar un nombre a los ejes:
>>> xlabel('abscisa')
>>> ylabel('ordenadas') Y después se da un título al gráfico:
>>> title('función cuadrada') Posteriormente, puede mostrar su gráfico:
>>> show() Observe que la curva será tanto más precisa cuando más puntos haya. Esto se hará cambiando el espacio lineal de inicio (y repitiendo todas las etapas):
>>> x = linspace(-5, 5, 101)
>>> x = linspace(-5, 5, 1001) A continuación se muestra el resultado:
2. Sintaxis de objeto
Podemos realizar exactamente el mismo tipo de operación con ayuda de una sintaxis de objeto:
x = linspace(-5, 5, 11)
y = x ** 2
fig = plt.figure()
axes = fig.add_axes([0, 0, 1, 1])
axes.plot(x, y, 'r')
axes.set_xlabel('abscisa')
axes.set_ylabel('ordenadas')
axes.set_title('función cuadrada') En IPython o IPythObservebook, este código será suficiente para mostrar el gráfico. También se puede registrar en un archivo:...
Introducción a Pandas
1. Presentación
Pandas es una librería Python especializada en el tratamiento, manipulación y análisis de datos.
Estos datos se organizan en form de un dataframe, que es una tabla organizada, como un archivo CSV. Las columnas de una tabla como esta, se corresponden con las variables y las filas a los individuos. Cuando los datos se organizan en una sola columna, se puede utilizar la noción de serie.
Para instalar Pandas, es suficiente con hacer:
$ pip install pandas 2. Series
Una serie es un dataframe que solo tienen una columna, comparable a una lista Python. También se crea a partir de una lista con esta:
>>> from pandas import Series
>>> s = Series([1, 1, 2, 3, 5, 8, 13]) Cada serie se asocia a un índice que, por defecto, se construye como el de las listas:
>>> s.index
RangeIndex(start=0, stop=7, step=1) De esta manera, se puede direccionar rápidamente un elemento de la serie, a partir de su índice:
>>> s[1]
1
>>> s[4]
5
>>> s[9]
KeyError: 9 También se puede extraer una subserie:
>>> s[2:5]
2 2
3 3
4 5
dtype: int64 Aquí vemos a la izquierda el índice y a la derecha el valor. Lo principal es que el índice asociado al valor, sigue siendo idéntico en lugar de volverse a crear sobre la marcha, como sería el caso para una lista. Observe que, como siempre, se parte del índice mínimo incluido en el índice máximo excluido. Observe también que, como sucede con NumPy, una serie se asocia a un tipo que se determina automáticamente, como sucede aquí o se indica durante la creación de la serie. En nuestro ejemplo, solo tenemos enteros, por lo tanto, tenemos un tipo entero. A continuación se muestran otros ejemplos:
>>> Series([1, 1, 2, 3, 5, 8, 13], dtype=float).dtype
dtype('float64')
>>> Series([1, 1., 2, 3, 5, 8, 13]).dtype
dtype('float64') En el primer caso el tipado es explícito, en el segundo caso es implícito y se debe al hecho de que hay un 1, que es la representación de un número en coma flotante.
Para terminar...
 Ediciones ENI Editorial | líder en informática
Ediciones ENI Editorial | líder en informática