Ordenar

Introducción

Este capítulo presenta la clasificación de datos comparables. Se considera una colección C de datos del mismo tipo T, cualquiera pero COMPARABLE. Queremos obtener una representación ordenada de los elementos de la colección. Lo más habitual es que los datos se organicen en una tabla. Aquí no buscamos clasificaciones de calidad, evaluadas según sus rendimientos, sino más bien un pretexto para la construcción razonada de algoritmos.

La sección «Especificar un algoritmo de orden» empieza por plantear el problema. Es la parte difícil del capítulo y se puede ignorar en la primera lectura. En particular, la especificación algorítmica completa de un algoritmo de orden impone la definición de los multiconjuntos invariables y de determinadas operaciones aplicables difíciles de especificar. La sección siguiente estudia algunos algoritmos habitualmente definidos en una iniciación a la algoritmia. La sección «Fusionar dos tablas ordenadas» muestra cómo fusionarlas para obtener una tabla ordenada nueva. Por último, la sección «Ejercicios» propone ejercicios más difíciles.

Especificar un algoritmo de orden

Esta sección está compuesta de dos partes. La primera presenta el problema del orden de datos comparables. La segunda estudia la poscondición de una clasificación. Es la parte verdaderamente difícil del capítulo y se puede ignorar en primera lectura.

1. Presentación del problema del orden

Sea t una tabla donde todos los componentes son de un tipo T derivado de COMPARABLE. Queremos un algoritmo que sustituya en t sus componentes en orden, por ejemplo, creciente. La siguiente figura representa una tabla de números enteros antes y después de ordenarla.

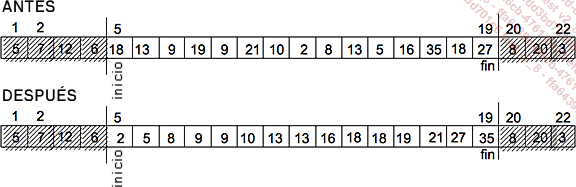
Como siempre, el algoritmo que hay que definir interviene en una parte especificada de la tabla, entre las celdas con los números inicio y fin. Los datos se sustituyen en orden creciente en la misma tabla, que se encuentra modificada por el algoritmo. Por lo tanto, se trata de escribir un procedimiento. Los datos de entrada son la tabla t y los números de los componentes de los extremos inicio y fin. La firma del procedimiento y su precondición se pueden especificar de la siguiente manera:

Algoritmo orden_ascendente  
    # Ordenar 't[inicio .. fin]' en orden creciente.  
  
Entrada 
    t: TABLA[T  COMPARABLE] # La tabla a ordenar 
    inicio, fin: ENTERO # Números de los componentes extremos a ordenar 
  
precondición  
    # 'inicio' y 'fin' son índices válidos de 't'  
    inicio ≤ fin => índice_válido(t, inicio) y índice_válido(t, fin) 
  
    # 't[inicio .. fin]' se ha inicializado  
    está_definido(t, inicio, fin)

El algoritmo está_definido es un predicado que devuelve VERDADERO si y solo si se ha inicializado la subtabla t[inicio .. fin].

Algoritmo 1: Especificaciones de está_definido

Algoritmo está_definido  
    # ¿'t[inicio .. fin]' se ha inicializado?  
  
Entrada 
    t: TABLA[T  COMPARABLE] # La tabla a explorar 
    inicio, fin: ENTERO # Números componentes...

Algunos algoritmos simples

Esta sección presenta algunos algoritmos sencillos que permiten ordenar los elementos de una tabla. La primera parte introduce una estrategia general natural de orden de los elementos de una tabla. En esta estrategia, la segunda parte presenta una primera solución estudiando un algoritmo que es a los algoritmos de ordenar lo que el cálculo de un factorial es al estudio de la recursividad: un ejercicio obligado. Desde el estricto punto de vista de la informática, los rendimientos de un algoritmo de este tipo son tan pobres que ningún informático serio ha soñado, ni por un momento, con usarlo en una situación real para ordenar un volumen de datos importante. Solo se sigue estudiando por sus propiedades pedagógicas. La tercera parte estudia una segunda solución. Es un algoritmo para ordenar por permutaciones que realiza unas pocas operaciones menos que el anterior. Una vez más, los razonamientos aplicados justifican el estudio de este algoritmo. La última parte presenta algunas variaciones del orden por permutaciones.

1. Orden por permutaciones: introducción

Sea una tabla t con componentes de tipo T que deriva de COMPARABLE. Queremos ordenarla en orden creciente. Esta operación consiste en llevar los valores grandes hacia lo «alto» de la tabla, hacia la celda con el número fin. De hecho, t[fin] contendrá el componente de mayor valor de t[inicio .. fin]. Una estrategia para ordenar consiste en llevar el valor máximo de t[inicio .. fin] a t[fin], donde estará en su ubicación definitiva. A continuación, el valor más alto de t[inicio .. fin - 1] se moverá a t[fin - 1], que será su posición definitiva y así sucesivamente. De esta manera, en cada etapa del cálculo, la tabla está dividida en dos subtablas: la parte «alta», que contiene los elementos más grandes y que no evolucionará más, y la parte «baja» que todavía no está ordenada.

Vamos a considerar, por ejemplo, la situación representada por la figura que aparece a continuación.

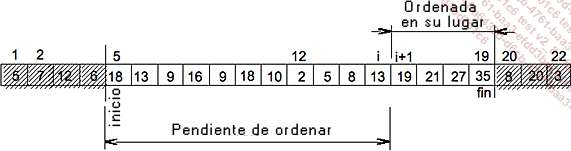
La parte etiquetada como «Ordenada en su lugar» reúne componentes que han adquirido su lugar definitivo y no se moverán después. Por eso es inútil explorar esta parte...

Fusionar dos tablas ordenadas

Sean dos tablas, t1 y t2, ordenadas en orden creciente. Queremos obtener una tabla Resultado del mismo tipo, ordenada en orden creciente, que agrupe los elementos de t1 y t2. La figura que aparece a continuación ilustra el efecto del algoritmo que vamos a estudiar.

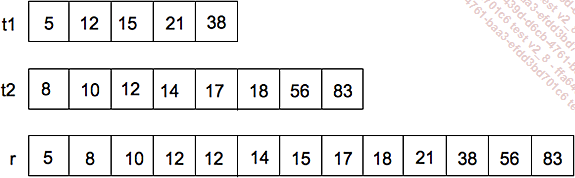
Observe que las dos tablas no tienen necesariamente la misma cantidad de elementos. La tabla resultado tendrá un número de componentes igual a la suma de los números de los componentes de t1 y t2. Los elementos idénticos en las dos tablas se repiten en la tabla resultado. Además, una misma tabla puede contener varios ejemplares de un elemento.

Si se fusiona t1 entre las celdas inicio1 y fin1 con t2 entre las celdas inicio2 y fin2, se obtiene una tabla resultado que tendrá fin1 - inicio1 + 1 + fin2 - inicio2 + 1 componentes. Para resolver este problema fácilmente, la sección siguiente empieza por introducir un tipo de datos nuevo: el vector. Se trata de una tabla donde están definidas operaciones aplicables particulares. La sección que la seguirá permitirá resolver el problema de la fusión de dos vectores.

1. Definición de un vector

Un vector es una subtabla de una tabla simple definida por dos índices, inicio y fin. También hay definidas operaciones aplicables a un vector para simplificar los algoritmos que usan estas estructuras de datos.

Un vector se define por:

tipo  
    VECTOR  
estructura 
    t: TABLA[T]   # Datos asociados al vector 
    inicio   : ENTERO # Primera celda del vector en t 
    fin      : ENTERO # Última celda del vector en t  
invariante 
    inicio ≤ fin  
    índice_válido(t, inicio)  
    índice_válido(t, fin)  
fin VECTOR

Un vector se declara como una tabla, especificando el tipo T de los datos que contiene y los números de las celdas de los extremos, como aquí:

...   
variable   
   v: VECTOR[ENTERO][-15, 30]   
...

Esta «instrucción» declara un vector v de números enteros, donde las celdas se numerarán...

Ejercicios

1. Ordenación por inserción dicotómica

Sea t una tabla de una sola línea (vector) de elementos de un tipo T que derivan de COMPARABLE, y que hay que ordenar en orden creciente. Cada elemento está insertado en su lugar dentro del resultado que se ha de obtener buscando su posición de inserción mediante el algoritmo dicotomía estudiado en el capítulo «Iteración».

Las ordenaciones presentes en la sección anterior de este capítulo «Algunos algoritmos simples» no han usado la ayuda de una tabla adicional para construir el resultado. Modifican la tabla que hay que ordenar para reordenar sus componentes. Aquí estudiamos los dos tipos de soluciones haciendo intervenir el método de inserción por dicotomía.

Ejercicio 4: Ordenación por inserción dicotómica

Sea t una tabla de una sola línea donde los componentes son de tipo T images/flechedroite.png

COMPARABLE.

1. Escribir primero las especificaciones del algoritmo que no usa la ayuda de otra tabla para calcular su resultado.

Así, los elementos de t están «ordenados en su lugar». Cuidar especialmente la precondición y la poscondición; no son fáciles de obtener, pero proporcionan una guía útil para la construcción del algoritmo.

2. Desarrollar el análisis completo de la solución...

Resumen

Este capítulo ha presentado la construcción de algunos algoritmos en el dominio del del orden de datos organizados en tablas. Primero hemos estudiado la especificación general de un algoritmo de orden que usa una tabla adicional para ordenar los datos. A continuación hemos presentado la definición de una estructura VECTOR, que permite iterar de manera simple en los datos. Esta estructura se ha usado para escribir un algoritmo de fusión en orden creciente de dos tablas ordenadas. Los ejercicios nos han permitido ir más lejos en la construcción de algoritmos, abordando el ordenamiento de tareas sometidas a restricciones de prioridad. La ambición de este capítulo no era el estudio del orden de los datos como problema general. Todo estudio serio, incluso restringido a algunas soluciones tipo debe ir acompañado de una evaluación de la complejidad de los algoritmos propuestos, lo que no sucede en este caso.