Simular
Introducción
Este capítulo se interesa por las técnicas que permiten hacer previsiones. Aunque los conceptos abordados son básicos, el contenido es fundamentalmente matemático. Los lectores a los que no les guste practicar estas actividades pueden pasar al capítulo siguiente.
Existen previsiones de distinta naturaleza y alcance. Podemos interesarnos por sucesos que se producirán inevitablemente en el futuro. Es el campo, por ejemplo, de las previsiones meteorológicas o de los métodos de cálculo que buscan determinar el recorrido de un cuerpo celeste en su trayectoria. Disponemos de un modelo matemático que describe, más o menos bien, la realidad de los fenómenos y que permite conocer su evolución por adelantado, en cierta medida. Entonces podemos tomar decisiones que regularán nuestro comportamiento. Podemos querer hacer previsiones sobre la evolución de un fenómeno que en la realidad es imposible poner en práctica. ¿Cómo se comportará la fauna de un curso de agua determinado en caso de contaminación masiva con hidrocarburos? ¿Cuáles son las consecuencias de un accidente de avión en un barrio determinado de una ciudad? Los fenómenos de los que se trata son destructivos y no se pueden provocar voluntariamente. La evolución a lo largo del tiempo de un proceso dinámico, pero...
Generar números pseudoaleatorios
En esta sección, estudiamos la generación de números pseudoaleatorios que luego se usarán en las otras secciones. Queremos disponer de una serie de números obtenida «al azar». Por el momento, esta expresión significa que el conocimiento de todos los ejemplares de los números ya obtenidos no permite determinar el valor del siguiente número que se va a obtener. Así, por ejemplo, cuando disponemos de una moneda bien equilibrada y la utilizamos para jugar a «cara o cruz», la serie de términos ya obtenidos no permite conocer el resultado de la próxima tirada. Todo lo que podemos decir es que este resultado será CRUZ con una probabilidad del 0,5 y CARA con la misma probabilidad. La serie de sucesos obtenida es aleatoria.
Es imposible preparar un generador automático de números aleatorios. Sin embargo, hay técnicas de cálculo que permiten obtener series que «imitan» los números obtenidos «al azar», en el sentido que hemos definido antes. Como estos generadores engendran los números con ayuda de una función determinista, se denominan «pseudoaleatorios». La primera sección estudia algunos ejemplos sencillos de generadores. Sin embargo, obtener una serie automática de números no es suficiente. Hay que disponer de pruebas que permitan asegurarse de que las series obtenidas «imitan bien el azar», es decir, que tienen las propiedades requeridas para sustituir a las series de números perfectamente aleatorios. La segunda sección muestra cómo realizar algunas pruebas sencillas en este tipo de series.
1. Algunos generadores
Para generar números «al azar», se origina una serie de números (xn)n>0 a partir de un número inicial dado x0. Una función matemática f permite calcular xn = f(xn-1). Entonces se obtiene una serie de números pseudoaleatorios porque el conocimiento de un elemento xi cualquiera de esta serie permite determinar cualquier elemento de la serie. Algunas pruebas de la sección siguiente mostrarán por qué y cuándo se puede aceptar que este tipo de series sustituyan a números al azar. Siguiendo la función f y la raíz x0 de la serie, se obtendrán resultados...
Juegos de azar
1. Simular una ruleta
Consideramos la ruleta esquemática que aparecen en el dibujo siguiente.
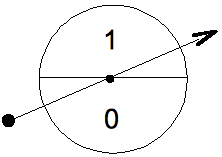
Simboliza el hecho de que los dos sucesos {0,1} tienen la misma probabilidad de salir: 0,5. Desde la sección anterior, sabemos obtener números aleatorios repartidos de manera uniforme en el intervalo ]0,1[. ¿Cómo obtener números enteros aleatorios en {0,1}cuando todos los sucesos tienen la misma probabilidad? Los números reales x que sabemos obtener son tales que 0 < x < 1. Entonces solo tenemos que sacar 0 para todo valor de x entre 0 y 0,5 o 1 para todo valor de x entre 0,5 y 1. La figura que aparece debajo representa lo que queremos obtener.
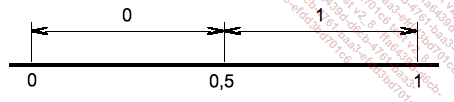
Los números generados tienen las mismas probabilidades. Por lo tanto, x pertenece al intervalo ]0; 0,5] con la probabilidad 0,5 y al intervalo [0,5; 1[ con la misma probabilidad. Si se añade 0,5 a x, el resultado pertenece al intervalo ]0,5; 1,5[ y la parte entera del resultado vale 0 o 1 con la probabilidad 0,5. Eso es lo que queremos. La figura siguiente representa esta situación.

Sea entero la función que devuelve la parte entera de su argumento. El principio algorítmico de simulación de una ruleta equitativa es sencillo:
...
variable
a: ALEA # La estructura mantenida por el generador
x:...Simulación del proceso dinámico
Esta sección estudia dos ejemplos cuya naturaleza debería permitir comprender en qué consiste la originalidad de los métodos de las secciones siguientes. Estos dos ejemplos solo aparecen como «segundones» de las siguientes secciones. El primer ejemplo estudia la propagación de un rumor en una población. El segundo muestra cómo representar un caso sencillo de carrera de persecución.
1. Propagación de un rumor
Sea una población humana homogénea de n individuos donde se propaga un rumor de boca a boca. Suponemos que toda persona que conoce el rumor lo propaga hasta que encuentra a una persona que ya lo conoce. Entonces deja de propagarlo. Nos interesa la evolución de los efectivos de las distintas clases de individuos dentro de la población. El rumor se extenderá, pero ¿llegará a todo el mundo? ¿Qué porcentaje de la población permanecerá ajena a este rumor?
Para realizar una simulación dinámica de la propagación, se hacen hipótesis sobre la frecuencia de los encuentros de cada tipo de individuo. Adoptamos ignora(t) como el efectivo de la población que ignora el rumor en el instante t. Igualmente, representamos como conoce(t) el efectivo de los que lo conocen pero ya no lo propagan, y como difunde(t) el efectivo de los que lo difunden. En todo momento t, tenemos:
conoce(t) = n - (ignora(t) + difunde(t)) Durante un intervalo de tiempo (una duración) ∆t, los efectivos ignora(t) y difunde(t) evolucionan en ignora(t + ∆t) y difunde(t + ∆t). Los contagios se producen durante encuentros del tipo ignora <-> difunde que son del número de ignora(t) x difunde(t) y la variación de los efectivos correspondientes para un ∆t pequeño es proporcional a este producto. Entonces podemos escribir:
ignora(t + ∆t) = ignora(t) - a x ignora(t) x difunde(t) Las inmunizaciones se producen durante encuentros del tipo...
Simulación estadística de fenómenos deterministas
En esta sección, proponemos ejercicios de escritura de algoritmos que muestran cómo estimar resultados perfectamente deterministas usando números pseudoaleatorios. Entonces buscamos obtener una estimación estadística de resultados que no dependen del azar. Los métodos implementados identifican métodos llamados Montecarlo como referencia al mundo de los juegos de azar que han hecho famosa a la ciudad del mismo nombre. Estos métodos aparecieron como herramientas de búsqueda durante la segunda guerra mundial para simular el comportamiento de los neutrones de las materias fisibles. Se emplean, por ejemplo, para calcular integrales múltiples denominadas integrales de configuración.
La sección «Calcular π» muestra cómo calcular una estimación del número π. El método usado es un caso particular de integrales definidas, presente en la sección «Evaluar una integral definida».
1. Calcular π
Dado un disco (D) de radio r. Sabemos calcular su área. Es A(D) = π x r2. Pero ¿cuánto vale π? Esta sección muestra cómo obtener una evaluación estadística del valor de π.
π es el área de un disco de radio r = 1. Este disco está inscrito en un cuadrado (C) de lado c = 2...
Simulación de fenómenos aleatorios
1. Cazar moscas
Esta sección podría titularse: ¡el azar al servicio de una neurosis!
Queremos capturar moscas para encerrarlas dentro de un frasco. Los motivos de un comportamiento de este tipo no están relacionados con este libro: adiestramiento, experimentación científica, etc. Después de cada captura, hay que abrir la tapa del frasco para encerrar a la siguiente mosca. Pero entonces, todas las moscas prisioneras, incluida la nueva, pueden escaparse, digamos con una probabilidad p. ¿Cuántas moscas hay que atrapar, de media, para obtener un número n de prisioneras? Se trata de simular un determinado número de este tipo de partidas de caza para obtener una estimación estadística de la cantidad media de moscas que hay que atrapar para constituir una colección de n ejemplares.
Está claro que la simulación, en la medida en que proporciona una estimación fiable del resultado esperado, es la única práctica experimental posible. Por supuesto, el problema es suficientemente sencillo como para ser resuelto de manera exacta mediante el cálculo, pero ese no es nuestro propósito: queremos escribir algoritmos de simulaciones.
|
Ejercicio resuelto 3: Simular una caza de moscas |
Para simular una captura, es suficiente con hacer girar la ruleta de dos sucesos que saca el suceso 1 con la probabilidad p y el suceso 0 con la probabilidad (1 - p). Se lanza la ruleta para cada mosca prisionera con el propósito de determinar si se escapa o no. Evidentemente, las moscas se escapan cuando la ruleta saca 1.
SimularNcazas para capturarnmoscas durante cada una de ellas. Estimar el número medio de moscas que hay que capturar.
Solución
Queremos simular la captura de n moscas. Sea caza el algoritmo que simula una partida de caza. Debe conocer el número n de moscas para capturar y la probabilidad p de fuga de una mosca capturada. Devuelve el número total de moscas capturadas para obtener n. Entonces, es una función cuya especificación viene dada por el algoritmo siguiente.
|
Algoritmo 7: Especificación de la función caza |
Algoritmo caza
# Una caza para capturar 'n' moscas. Cada una puede escaparse
# con la probabilidad 'p'. Devuelve...Resumen
En este capítulo se han propuesto algunas actividades sencillas que permiten simular procesos deterministas o aleatorios. A veces, las fórmulas utilizadas pueden parecer impresionantes, pero el contenido matemático sigue siendo de un nivel elemental. Por el contrario, a menudo, los algoritmos propuestos son difíciles de especificar de manera formal y las verificaciones y las pruebas de los programas son especialmente difíciles porque los resultados son imprevisibles. Todos los problemas propuestos se resuelven fácilmente mediante el cálculo, y así es posible verificar la coherencia de los resultados producidos por los programas informáticos con los que dan los cálculos matemáticos.
 Ediciones ENI Editorial | líder en informática
Ediciones ENI Editorial | líder en informática